Statistika Bisnis Sesi 12

Sesi 12 – Analisis Regresi Linier (Simple & Multiple Regression)

Deskripsi Sesi

Sesi ini membahas analisis regresi linier sebagai alat utama dalam riset bisnis kuantitatif untuk memodelkan, menjelaskan, dan memprediksi hubungan antar variabel numerik. Mahasiswa tidak hanya belajar cara menjalankan regresi di Microsoft Excel, tetapi juga memahami logika metode, asumsi, interpretasi hasil, serta keterbatasannya dalam konteks bisnis nyata.

Materi disusun untuk menghindari penggunaan regresi secara mekanis tanpa pemahaman metodologis, yang merupakan kesalahan umum dalam penulisan skripsi.

---

Learning Objectives

Setelah mengikuti sesi ini, mahasiswa mampu:

1. Menjelaskan perbedaan korelasi dan regresi
2. Memahami konsep regresi linier sederhana dan berganda
3. Menafsirkan makna intercept (b₀) dan slope (b₁)
4. Mengevaluasi asumsi-asumsi regresi linier
5. Melakukan dan membaca output regresi menggunakan Microsoft Excel
6. Mengaitkan hasil regresi dengan pengambilan keputusan bisnis

---

1. Korelasi vs Regresi

Scatter plot digunakan untuk melihat pola hubungan antara dua variabel.
Namun:

• Korelasi hanya mengukur kekuatan hubungan linier
• Regresi digunakan untuk:
  • memprediksi nilai variabel dependen
  • menjelaskan pengaruh perubahan variabel independen terhadap variabel dependen

📌 Penegasan penting
Korelasi tidak menyiratkan hubungan sebab-akibat, sedangkan regresi dibangun atas asumsi hubungan kausal yang didukung teori dan logika bisnis levine_smume6_ppt13

---

2. Konsep Dasar Regresi Linier

2.1 Regresi Linier Sederhana

Digunakan ketika terdapat satu variabel independen (X) dan satu variabel dependen (Y).

Model populasi:$$Y_i = \beta_0 + \beta_1 X_i + \varepsilon_i$$

Model estimasi:$$\hat{Y} = b_0 + b_1 X$$

• b₀ (intercept): nilai rata-rata Y saat X = 0
• b₁ (slope): perubahan rata-rata Y akibat kenaikan 1 unit X

📌 Dalam konteks bisnis, makna b₁ jauh lebih penting daripada b₀, terutama jika X = 0 tidak realistis secara empiris levine_smume6_ppt13

---

2.2 Regresi Linier Berganda

Digunakan ketika lebih dari satu variabel independen memengaruhi Y.

$$Y = b_0 + b_1 X_1 + b_2 X_2 + \cdots + b_k X_k + \varepsilon$$

📌 Regresi berganda bukan sekadar menambah variabel, tetapi menuntut:

• justifikasi teoritis
• logika bisnis yang kuat
• definisi operasional variabel yang jelas

---

3. Metode Estimasi: Least Squares

Koefisien regresi diperoleh dengan metode kuadrat terkecil, yaitu meminimalkan jumlah kuadrat selisih antara nilai aktual dan nilai prediksi.

$$\min \sum (Y_i – \hat{Y}_i)^2$$

Hasil estimasi inilah yang ditampilkan dalam output Excel, bukan nilai “sebenarnya” populasi levine_smume6_ppt13

---

4. Evaluasi Model: Variasi dan Koefisien Determinasi

4.1 Komponen Variasi

• SST (Total Variation)
• SSR (Explained Variation)
• SSE (Unexplained Variation)

$$SST = SSR + SSE$$

4.2 Koefisien Determinasi (R²)

R² menunjukkan proporsi variasi Y yang dapat dijelaskan oleh X.

📌 R² tinggi tidak otomatis berarti model baik, jika:

• asumsi dilanggar
• variabel tidak relevan secara bisnis

---

5. Asumsi Regresi Linier (L.I.N.E)

Regresi linier mensyaratkan:

• Linearity → hubungan X–Y bersifat linier
• Independence → error saling bebas
• Normality → error berdistribusi normal
• Equal Variance (Homoscedasticity) → varians error konstan

Evaluasi dilakukan melalui analisis residual, termasuk:

• residual vs X
• histogram residual
• normal probability plot
• uji Durbin–Watson (untuk data runtut waktu) levine_smume6_ppt13

---

6. Pengujian Hipotesis dalam Regresi

6.1 Uji t (Parsial)

Digunakan untuk menguji apakah masing-masing koefisien regresi berbeda dari nol.

$$H_0: \beta_j = 0 \quad vs \quad H_1: \beta_j \neq 0$$

6.2 Uji F (Simultan)

Digunakan untuk menilai apakah model regresi secara keseluruhan bermakna.

📌 Kesalahan umum mahasiswa
Menarik kesimpulan hanya dari p-value, tanpa memahami konteks variabel dan model.

---

7. Estimasi dan Prediksi dalam Regresi

Regresi digunakan untuk dua tujuan berbeda:

1. Confidence Interval → estimasi rata-rata Y
2. Prediction Interval → prediksi nilai individu Y

Prediction interval selalu lebih lebar, karena mencakup ketidakpastian individual

---

8. Implementasi Regresi Menggunakan Microsoft Excel

Langkah umum:

1. Menyusun data dalam kolom (Y dan X)
2. Mengaktifkan Data Analysis ToolPak
3. Memilih Regression
4. Menentukan:
   • Input Y Range
   • Input X Range
5. Membaca output regresi

📌 Fokus pembelajaran bukan pada klik, tetapi pada interpretasi dan implikasi bisnis.

---

9. Pitfalls dalam Penggunaan Regresi

Beberapa jebakan umum:

• Mengabaikan asumsi regresi
• Menggunakan regresi tanpa pemahaman konteks bisnis
• Melakukan ekstrapolasi di luar rentang data
• Menganggap regresi sebagai “mesin pencari signifikansi”

Strategi utama:

Mulai dari visualisasi, cek asumsi, baru melakukan inferensi statistik

Sesi 12 (Tambahan Praktik): Korelasi & Regresi Linier Sederhana di Microsoft Excel

A. Menyiapkan Data di Excel

1. Buka Microsoft Excel
2. Buat tabel dengan format kolom berikut:

A	B	C
Toko	Luas_Toko	Penjualan_Bulanan
1	50	18
2	70	22
…	…	…

📌 Aturan penting

• Setiap baris = satu observasi
• Tidak ada sel kosong
• Variabel X dan Y harus numerik

---

B. Menghitung Korelasi di Excel

Cara 1: Menggunakan Fungsi

1. Klik sel kosong
2. Ketik:

=CORREL(B2:B11, C2:C11)

3. Tekan Enter

Interpretasi singkat

• Nilai positif → hubungan searah
• Nilai mendekati 1 → hubungan kuat

📌 Catatan dosen
Korelasi tidak menunjukkan sebab–akibat, hanya hubungan.

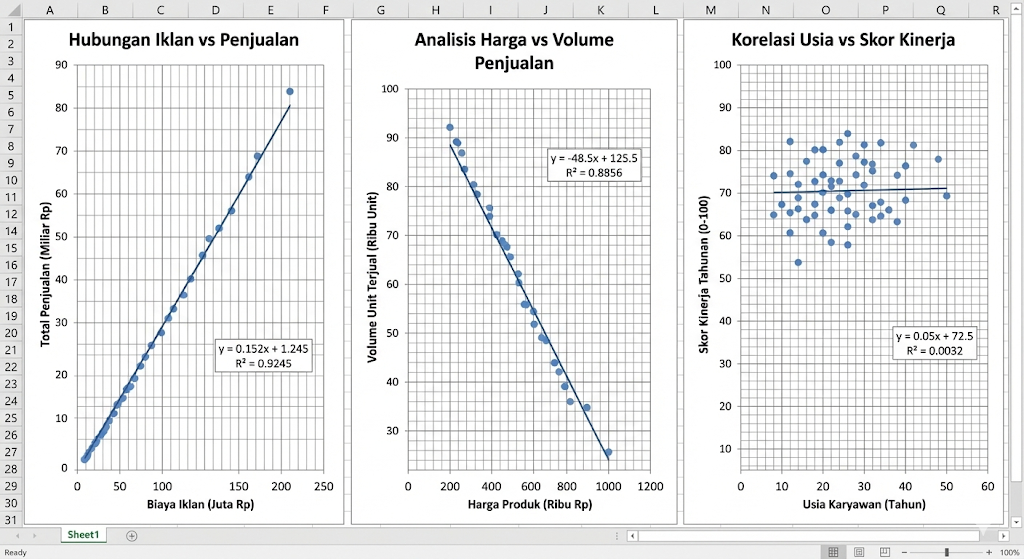
1️⃣ Hubungan Iklan vs Penjualan

Penjelasan
Grafik menunjukkan hubungan positif yang sangat kuat antara biaya iklan dan total penjualan. Titik-titik data membentuk pola linier menaik dengan nilai $R^2 = 0{,}9245$R2=0,9245, yang berarti sekitar 92,45% variasi penjualan dapat dijelaskan oleh biaya iklan. Hal ini mengindikasikan bahwa peningkatan anggaran iklan berkaitan erat dengan peningkatan penjualan.

Catatan metodologis
Grafik ini menunjukkan korelasi yang kuat dan layak dilanjutkan ke analisis regresi linier sederhana untuk menguji pengaruh secara statistik.

Caption
Gambar X. Scatter plot hubungan biaya iklan dan total penjualan.

---

2️⃣ Analisis Harga vs Volume Penjualan

Penjelasan
Grafik menunjukkan hubungan negatif yang kuat antara harga produk dan volume penjualan. Garis regresi memiliki kemiringan negatif dengan nilai $R^2 = 0{,}8856$R2=0,8856, yang menunjukkan bahwa kenaikan harga cenderung diikuti oleh penurunan volume penjualan. Hubungan ini konsisten dengan konsep dasar elastisitas permintaan dalam ekonomi.

Catatan metodologis
Korelasi negatif yang kuat ini menunjukkan bahwa harga merupakan faktor penting dalam menentukan volume penjualan dan relevan untuk analisis prediktif.

Caption
Gambar Y. Scatter plot hubungan harga produk dan volume penjualan.

---

3️⃣ Korelasi Usia vs Skor Kinerja

Penjelasan
Grafik menunjukkan hubungan yang sangat lemah antara usia karyawan dan skor kinerja. Nilai $R^2 = 0{,}0032$R2=0,0032 mengindikasikan bahwa usia hampir tidak menjelaskan variasi kinerja karyawan. Sebaran titik yang acak menunjukkan tidak adanya pola hubungan yang berarti.

Catatan metodologis
Dalam kasus ini, usia tidak layak digunakan sebagai prediktor utama kinerja, dan peneliti perlu mempertimbangkan variabel lain seperti pengalaman kerja, motivasi, atau pelatihan.

Caption
Gambar Z. Scatter plot hubungan usia karyawan dan skor kinerja.

---

🔑 Ringkasan Pembelajaran (1 paragraf)

Ketiga grafik menunjukkan bahwa korelasi dapat bersifat positif, negatif, atau lemah, tergantung pada konteks variabel yang dianalisis. Korelasi digunakan sebagai alat eksplorasi awal untuk memahami pola hubungan antar variabel, namun tidak dapat digunakan untuk menyimpulkan hubungan sebab-akibat tanpa analisis lanjutan seperti regresi.

---

C. Mengaktifkan Data Analysis Add-in (WAJIB)

Jika menu Data Analysis belum muncul:

1. Klik File → Options
2. Pilih Add-ins
3. Pada bagian bawah:
   • Manage: Excel Add-ins
   • Klik Go
4. Centang Analysis ToolPak
5. Klik OK

➡️ Menu Data Analysis akan muncul di tab Data

---

D. Melakukan Regresi Linier Sederhana di Excel

Langkah-langkah:

1. Klik tab Data
2. Pilih Data Analysis
3. Pilih Regression → klik OK

Isi Parameter:

• Input Y Range
  → Kolom Penjualan_Bulanan (C1:C11)
• Input X Range
  → Kolom Luas_Toko (B1:B11)
• Centang Labels (jika ada judul kolom)
• Pilih Output Range atau New Worksheet
• Klik OK

---

E. Output yang Perlu Diperhatikan (JANGAN SEMUA)

Mahasiswa cukup fokus pada 4 hal ini:

1. R Square
   → seberapa besar variasi Y dijelaskan X
2. Significance F
   → apakah model signifikan
3. Koefisien X (Slope)
   → arah dan besar pengaruh
4. Scatter plot + garis regresi

📌 Stop di sini. Tidak perlu bahas yang lain dulu.

---

F. Kalimat Interpretasi (Siap Pakai)

Hasil analisis regresi linier sederhana menunjukkan bahwa luas toko berpengaruh positif terhadap penjualan bulanan. Model regresi signifikan pada tingkat signifikansi 5%, sehingga dapat disimpulkan bahwa luas toko memiliki pengaruh yang bermakna terhadap penjualan.

---

G. Catatan Pedagogis untuk Mahasiswa

• Korelasi → hubungan
• Regresi → pengaruh
• Excel → alat bantu, bukan penentu kesimpulan

---

---

---

Contoh–Contoh Regresi Linier (Konteks Indonesia)

Contoh 1 – Regresi Linier Sederhana (Ritel / UMKM)

Kasus
Seorang pemilik minimarket ingin mengetahui apakah luas toko berpengaruh terhadap penjualan bulanan.

Variabel

• Y (Penjualan Bulanan): total penjualan per bulan (Rp juta)
• X (Luas Toko): luas lantai toko (m²)

Model$$\text{Penjualan} = b_0 + b_1(\text{Luas Toko})$$

Interpretasi
Jika koefisien $b_1$b1​ bernilai positif dan signifikan, maka semakin luas toko, semakin besar potensi penjualan.

📌 Catatan pembelajaran
Model ini cocok sebagai analisis awal, tetapi belum mempertimbangkan faktor penting lain seperti promosi atau lokasi.

---

Contoh 2 – Regresi Linier Berganda (Ritel Modern Indonesia)

Kasus
Manajemen ritel ingin mengetahui faktor yang memengaruhi penjualan bulanan.

Variabel

• Y: Penjualan Bulanan (Rp juta)
• X₁: Luas Toko (m²)
• X₂: Biaya Promosi (Rp juta/bulan)

Model$$\text{Penjualan} = b_0 + b_1(\text{Luas Toko}) + b_2(\text{Biaya Promosi})$$

Interpretasi

• $b_1 > 0$b1​>0: toko lebih luas → penjualan meningkat
• $b_2 > 0$b2​>0: promosi lebih intens → penjualan meningkat

📌 Makna bisnis
Ekspansi fisik harus dibarengi promosi, tidak cukup mengandalkan ukuran toko saja.

---

Contoh 3 – Regresi dalam Layanan Publik (Indonesia)

Kasus
Sebuah kantor pelayanan publik ingin menganalisis pengaruh waktu layanan terhadap jumlah pengaduan masyarakat.

Variabel

• Y: Jumlah Pengaduan per Bulan
• X₁: Rata-rata Waktu Layanan (menit)
• X₂: Jumlah Petugas Layanan

Model$$\text{Pengaduan} = b_0 + b_1(\text{Waktu Layanan}) + b_2(\text{Jumlah Petugas})$$

Interpretasi

• Waktu layanan yang lebih lama → pengaduan meningkat
• Penambahan petugas → pengaduan menurun

📌 Catatan metodologis
Jika Y berupa jumlah kejadian kecil, mahasiswa bisa diarahkan ke regresi Poisson (materi lanjutan).

---

Contoh 4 – Regresi di Dunia Pendidikan (Kampus Indonesia)

Kasus
Dosen ingin menganalisis faktor yang memengaruhi nilai akhir mahasiswa.

Variabel

• Y: Nilai Akhir Mata Kuliah
• X₁: Kehadiran (%)
• X₂: Nilai Tugas
• X₃: Nilai UTS

Model$$\text{Nilai Akhir} = b_0 + b_1(\text{Kehadiran}) + b_2(\text{Tugas}) + b_3(\text{UTS})$$

📌 Penegasan penting

• Semua variabel numerik dan kontinu
• Regresi tepat digunakan

Jika Y diubah menjadi:

• Lulus / Tidak Lulus → regresi logistik
• Kepuasan kuliah → regresi ordinal

---

Contoh Kesalahan Umum Mahasiswa Indonesia (SALAH vs BENAR)

❌ SALAH

Menggunakan regresi linier untuk variabel kepuasan (1–5) tanpa penjelasan.

✅ BENAR

Menjelaskan bahwa data Likert diperlakukan sebagai interval atau menggunakan regresi ordinal.

---

Kalimat Siap Tempel (Gaya Bab IV Indonesia)

Berdasarkan hasil analisis regresi linier berganda, diperoleh bahwa luas toko dan biaya promosi berpengaruh positif terhadap penjualan bulanan. Model regresi secara keseluruhan signifikan pada tingkat signifikansi 5%, sehingga dapat disimpulkan bahwa variabel independen secara simultan memengaruhi variabel dependen.

---

Catatan Dosen (PENTING)

Sesi ini menegaskan bahwa regresi linier adalah alat pemodelan, bukan sekadar teknik statistik. Model yang baik bukan yang paling kompleks, tetapi yang paling masuk akal secara metodologis dan substantif.
Regresi bukan soal rumus atau software, tetapi soal kecocokan metode dengan realitas data Indonesia.

Referensi Utama (APA Style)

Levine, D. M., Stephan, D. F., Krehbiel, T. C., & Berenson, M. L. (2017). Statistics for managers using Microsoft Excel (8th ed.). Pearson. levine_smume6_ppt13