Dari Konsep, Logika Metode, hingga Implementasi Menggunakan Microsoft Excel
December 30, 2025
oleh Aurino Djamaris
Pendahuluan
Regresi linear merupakan salah satu teknik analisis kuantitatif yang paling sering digunakan dalam penelitian bisnis. Namun, dalam praktiknya, regresi kerap digunakan secara mekanis—sekadar menjalankan perintah di Excel—tanpa pemahaman yang memadai mengenai logika data, asumsi statistik, dan makna hasil analisis.
Artikel ini membahas regresi linier sederhana dan regresi linier berganda secara konseptual dan praktis, dilengkapi dengan data aktual, grafik, perbandingan error (MSE), serta lampiran file Excel, agar mahasiswa memahami mengapa dan bagaimana regresi digunakan secara benar.
1. Konsep Dasar Regresi Linear
1.1 Apa Itu Regresi Linear Berganda?
Regresi linear berganda digunakan untuk menganalisis pengaruh lebih dari satu variabel independen (X) terhadap satu variabel dependen (Y) yang bersifat numerik dan kontinu.
Secara umum, model regresi berganda dituliskan sebagai:
dengan:
- Y = variabel dependen
- X₁, X₂, … = variabel independen
- b₀ = konstanta
- b₁, b₂, … = koefisien regresi
- ε = error
📌 Penegasan penting
Regresi bukan alat untuk “mencari angka signifikan”, melainkan alat untuk memodelkan hubungan antar variabel.
1.2 Kapan Regresi Linear Tepat Digunakan?
Regresi linear tepat digunakan jika dan hanya jika:
- variabel dependen bersifat numerik dan kontinu,
- variabel independen numerik atau dapat diperlakukan sebagai numerik,
- tujuan penelitian adalah menguji pengaruh atau hubungan,
- terdapat definisi operasional variabel yang jelas.
❌ Regresi tidak tepat digunakan jika:
- variabel dependen bersifat nominal/kategorik,
- data murni ordinal tanpa justifikasi,
- tujuan penelitian adalah eksplorasi makna atau pengalaman (kualitatif).
2. Data Aktual Penelitian
Penelitian ini menggunakan data dari 10 toko, dengan variabel:
- Y (Monthly Sales) → penjualan bulanan
- X₁ (Floor Space) → luas area toko
- X₂ (Advertising Expenditure) → pengeluaran iklan
Struktur Data Aktual
| Store | Floor Space (X₁) | Advertising (X₂) | Monthly Sales (Y) |
|---|---|---|---|
| 1 | 3050 | 350 | 20100 |
| 2 | 1300 | 980 | 14900 |
| 3 | 1890 | 830 | 16800 |
| 4 | 1750 | 760 | 9100 |
| 5 | 1010 | 930 | 15500 |
| 6 | 2690 | 770 | 26700 |
| 7 | 4210 | 440 | 34600 |
| 8 | 1950 | 570 | 7200 |
| 9 | 2830 | 310 | 21800 |
| 10 | 2030 | 920 | 23400 |
📌 Catatan penting
Semua variabel bersifat numerik dan kontinu, sehingga memenuhi syarat penggunaan regresi linear.
3. Regresi Linier Sederhana (Simple Regression)
Pada regresi linier sederhana, hanya digunakan satu variabel independen, yaitu Floor Space (X₁), untuk memprediksi penjualan bulanan.
3.1 Hasil Utama
- Dihasilkan nilai forecast untuk setiap toko
- Error dihitung sebagai:
Contoh hasil:
| Store | Forecast | Error |
|---|---|---|
| 1 | 24195 | -4095 |
| 4 | 15542 | -6442 |
| 8 | 16874 | -9674 |
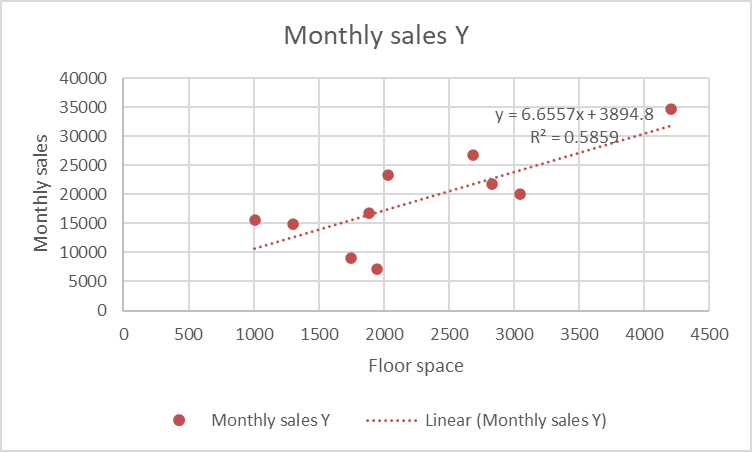
Grafik menunjukkan hubungan positif antara luas toko (Floor Space) dan penjualan bulanan (Monthly Sales). Garis regresi linier mengindikasikan bahwa semakin besar luas toko, penjualan cenderung meningkat. Nilai R² = 0,586 menunjukkan bahwa sekitar 58,6% variasi penjualan dapat dijelaskan oleh luas toko, sementara sisanya dipengaruhi faktor lain. Hal ini menandakan bahwa regresi linier sederhana belum sepenuhnya akurat dan perlu pengembangan model lebih lanjut.
3.2 Akurasi Model
Mean Squared Error (MSE):
📌 Makna
Dengan hanya satu variabel independen, model belum mampu menjelaskan variasi penjualan secara memadai. Error relatif besar dan tidak stabil.
4. Regresi Linier Berganda (Multiple Regression)
Pada regresi berganda, digunakan dua variabel independen sekaligus:
- X₁: Floor Space
- X₂: Advertising Expenditure
4.1 Persamaan Regresi
Interpretasi:
- setiap tambahan 1 unit luas toko meningkatkan penjualan rata-rata sebesar 11.42,
- setiap tambahan 1 unit biaya iklan meningkatkan penjualan rata-rata sebesar 23.41.
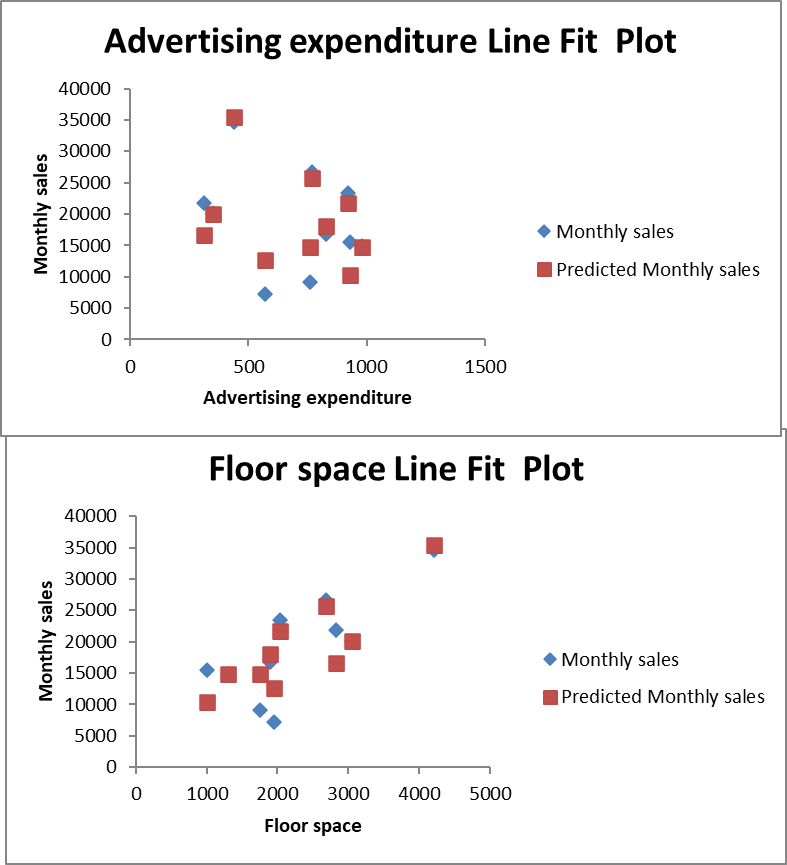
Persamaan regresi menunjukkan bahwa penjualan bulanan dipengaruhi secara positif oleh luas toko dan pengeluaran iklan. Koefisien yang lebih besar pada variabel advertising expenditure (X₂) mengindikasikan kontribusi yang relatif lebih kuat dibandingkan luas toko (X₁). Grafik line fit memperlihatkan bahwa nilai prediksi mengikuti pola data aktual, menandakan bahwa regresi berganda memberikan estimasi yang lebih baik dibandingkan regresi sederhana.Grafik line fit menunjukkan bahwa nilai prediksi lebih mendekati data aktual dibandingkan regresi sederhana.
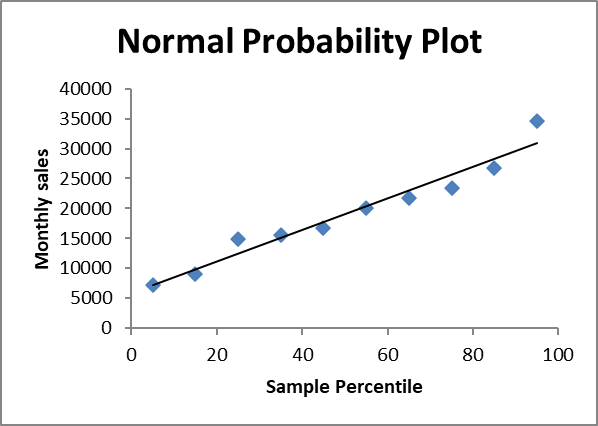
Normal Probability Plot yang menunjukkan sebaran data penjualan bulanan relatif mengikuti garis lurus, mengindikasikan distribusi data mendekati normal.
4.2 Akurasi Model
Contoh hasil prediksi:
| Store | Forecast | Error |
|---|---|---|
| 1 | 20036 | 64 |
| 2 | 14809 | 91 |
| 6 | 25760 | 940 |
| 7 | 35386 | -786 |
Mean Squared Error (MSE):
📌 Perbandingan kunci
- MSE regresi berganda jauh lebih kecil,
- model berganda lebih akurat dan stabil.
5. Kaitan dengan Uji Signifikansi (ANOVA)
Model regresi berganda didukung oleh:
- nilai F signifikan,
- Significance F < 0.05.
Artinya:
model regresi secara keseluruhan bermakna secara statistik,
bukan terjadi secara kebetulan.
6. Interpretasi Bisnis
Penurunan MSE menunjukkan bahwa:
- penjualan tidak hanya dipengaruhi oleh luas toko,
- iklan berperan signifikan dalam meningkatkan penjualan.
Implikasi bisnis:
- ekspansi toko perlu dibarengi strategi promosi,
- mengandalkan satu faktor saja menghasilkan prediksi yang lemah.
7. Pembelajaran Metodologis untuk Mahasiswa
Dari studi kasus ini, mahasiswa diharapkan memahami bahwa:
- Regresi bukan sekadar mencari koefisien,
- Kualitas model dinilai dari akurasi dan error, bukan hanya signifikansi,
- Penambahan variabel harus berdasarkan logika bisnis, bukan asal banyak.
Kesimpulan
Regresi linier sederhana cocok untuk eksplorasi awal,
namun regresi linier berganda memberikan model yang lebih realistis untuk pengambilan keputusan bisnis.
Model yang baik bukan yang paling sederhana,
tetapi yang paling mampu menjelaskan realitas bisnis.
Lampiran Praktik
📎 File Excel latihan:
📎 Unduh File Latihan: Multiple Regresion.xlsx
(File berisi data, perhitungan regresi, forecast, error, dan MSE)
Penjelasan Output Regresi Linier Sederhana
Analisis regresi linier sederhana dilakukan untuk menguji hubungan antara luas toko (Floor Space) sebagai variabel independen (X) dan penjualan bulanan (Monthly Sales) sebagai variabel dependen (Y). Output regresi yang dihasilkan oleh Microsoft Excel dapat dijelaskan sebagai berikut.
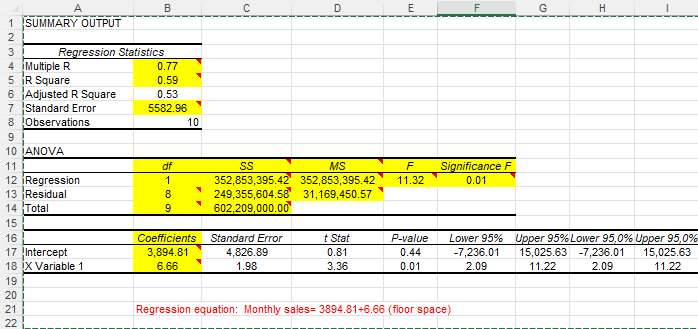
1. Regression Statistics
| Indikator | Nilai | Interpretasi |
|---|---|---|
| Multiple R | 0.77 | Menunjukkan hubungan yang cukup kuat dan positif antara luas toko dan penjualan bulanan |
| R Square | 0.59 | Sekitar 59% variasi penjualan bulanan dapat dijelaskan oleh luas toko |
| Adjusted R Square | 0.53 | Nilai R² yang telah disesuaikan dengan jumlah sampel |
| Standard Error | 5,582.96 | Rata-rata kesalahan prediksi model |
| Observations | 10 | Jumlah observasi (toko) yang dianalisis |
📌 Makna penting
Nilai R² sebesar 0.59 menunjukkan bahwa model memiliki daya jelas sedang, namun masih terdapat 41% variasi penjualan yang dijelaskan oleh faktor lain di luar model.
2. Tabel ANOVA (Uji Signifikansi Model)
| Sumber | df | SS | MS | F | Significance F |
|---|---|---|---|---|---|
| Regression | 1 | 352,853,395.42 | 352,853,395.42 | 11.32 | 0.01 |
| Residual | 8 | 249,355,604.58 | 31,169,450.57 | ||
| Total | 9 | 602,209,000.00 |
Interpretasi ANOVA
- Nilai F = 11.32
- Nilai Significance F = 0.01
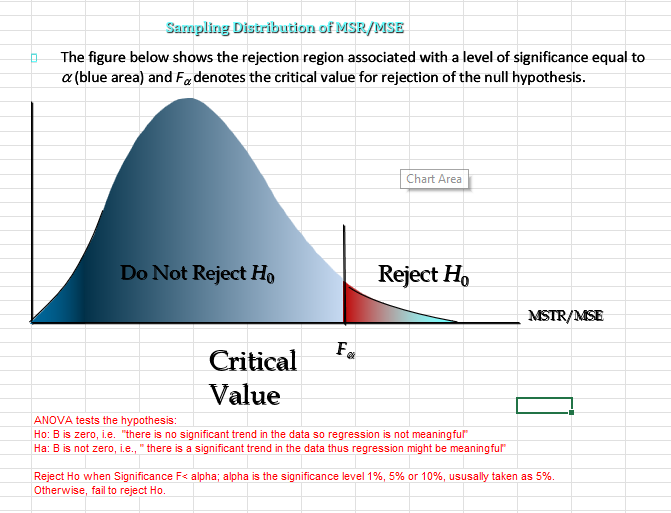
Karena Significance F < 0.05, maka:
H₀ ditolak, sehingga model regresi secara keseluruhan signifikan secara statistik.
📌 Artinya, luas toko secara bersama-sama memiliki hubungan yang bermakna dengan penjualan bulanan, dan model tidak terbentuk secara kebetulan.
3. Koefisien Regresi (Uji Parsial)
| Variabel | Koefisien | t Stat | P-value | Interpretasi |
|---|---|---|---|---|
| Intercept | 3,894.81 | 0.81 | 0.44 | Tidak signifikan |
| Floor Space (X₁) | 6.66 | 3.36 | 0.01 | Signifikan |
Interpretasi Koefisien
- Koefisien 6.66 menunjukkan bahwa setiap penambahan 1 unit luas toko akan meningkatkan penjualan bulanan rata-rata sebesar 6.66 unit, dengan asumsi faktor lain konstan.
- Nilai p-value = 0.01 < 0.05 menunjukkan bahwa pengaruh luas toko terhadap penjualan signifikan secara statistik.
- Intercept tidak signifikan, namun hal ini tidak menjadi masalah utama, karena fokus analisis terletak pada koefisien variabel independen.
4. Persamaan Regresi
Berdasarkan hasil analisis, persamaan regresi linier sederhana yang diperoleh adalah:Monthly Sales=3894.81+6.66(Floor Space)
Persamaan ini digunakan untuk memprediksi penjualan bulanan berdasarkan luas toko.
5. Kesimpulan Analisis
Berdasarkan hasil regresi linier sederhana dapat disimpulkan bahwa:
- Luas toko memiliki pengaruh positif dan signifikan terhadap penjualan bulanan.
- Model regresi signifikan secara statistik, namun belum sepenuhnya menjelaskan variasi penjualan.
- Diperlukan penambahan variabel lain (misalnya pengeluaran iklan) untuk meningkatkan akurasi model.
6. Catatan Metodologis untuk Mahasiswa
- Signifikan ≠ akurat → tetap perlu melihat error dan MSE
- Regresi sederhana cocok sebagai analisis awal (baseline model)
- Pengembangan model dapat dilakukan melalui regresi berganda
📌 Kalimat Siap Pakai (Bab IV Skripsi)
Berdasarkan hasil uji F diperoleh nilai Significance F sebesar 0.01 yang lebih kecil dari tingkat signifikansi 5%, sehingga model regresi dinyatakan signifikan secara statistik. Variabel luas toko berpengaruh positif dan signifikan terhadap penjualan bulanan.
Penulis
Aurino Djamaris
Referensi (APA Style)
Levine, D. M., Stephan, D. F., Krehbiel, T. C., & Berenson, M. L. (2017). Statistics for managers using Microsoft Excel (8th ed.). Pearson.
Categories: Riset Bisnis, Statistika Bisnis