Mencari Rute Paling Cepat: Model Jalur Terpendek (Shortest Path)
Diadaptasi dari Bab V modul “Pemanfaatan Excel-Solver Untuk Pengambilan Keputusan” (Aurino Djamaris).
Di dunia logistik, waktu adalah uang. Memilih rute yang salah untuk armada pengiriman tidak hanya membuang waktu, tetapi juga membengkakkan biaya bahan bakar. Lalu, bagaimana cara mencari jalan paling singkat dari satu titik awal ke titik tujuan yang melewati banyak persimpangan rute alternatif?
Inilah saatnya kita menggunakan kemampuan analitik Solver melalui Model Jalur Terpendek (Shortest Path)[cite: 128].
Konsep Jaringan Rute (Network)
Dalam panduan Bapak Aurino, kita membayangkan sebuah peta rute sebagai jaringan[cite: 128]:
- Node (Simpul): Titik singgah atau persimpangan kota (misalnya: S, A, B, C, D, E, dan T)[cite: 129]. Terdapat titik awal S (Start) dan titik tujuan akhir T (Target)[cite: 128].
- Arc (Jalur): Jalanan yang menghubungkan antar simpul tersebut (misalnya: jalan dari S ke A, jalan S ke B, dll.)[cite: 130].
Tujuan kita: Meminimalkan Total Jarak tempuh dari node S menuju node T[cite: 140].
Langkah Praktis di Excel
Langkah 1: Menyusun Tabel Jaringan
Buatlah tabel yang mendata seluruh rute (Jalur dari – ke) beserta Jarak-nya. Di sebelahnya, siapkan satu kolom kosong bernama Jalur (Keputusan).
Sama seperti Model Penugasan di Bagian 5, kolom keputusan ini nantinya hanya akan berisi angka 1 (Ya, ini rute yang dilewati) atau 0 (Tidak dilewati)[cite: 134, 135].

Langkah 2: Konsep Arus Bersih (Net Flow)
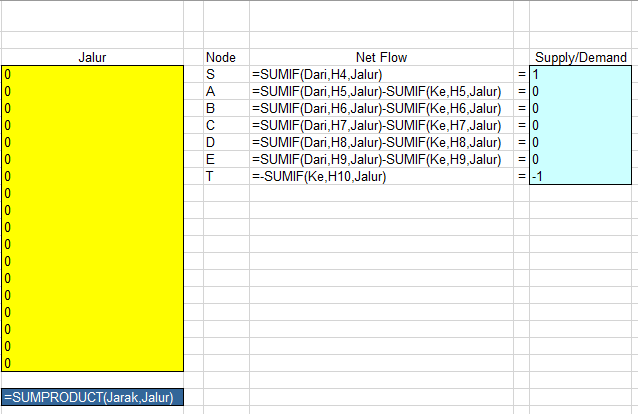
Ini adalah kunci utama dari model jaringan. Kita harus memastikan rute yang dipilih saling menyambung dan tidak terputus di tengah jalan. Kita menggunakan rumus SUMIF untuk menghitung Net Flow (Arus Keluar – Arus Masuk) setiap persimpangan (Node)[cite: 136, 142]:
- Titik Awal (S): Hanya boleh ada rute yang keluar (Net Flow harus = 1)[cite: 137].
- Titik Akhir (T): Hanya boleh menerima rute yang masuk (Net Flow harus = -1)[cite: 138].
- Titik Singgah (A, B, C, D, E): Mobil hanya lewat, jadi jumlah yang masuk harus sama dengan jumlah yang keluar (Net Flow harus = 0)[cite: 139].
Untuk total jarak, gunakan fungsi andalan kita: =SUMPRODUCT(Kolom_Jarak, Kolom_Jalur)[cite: 148].
Langkah 3: Atur Parameter Solver
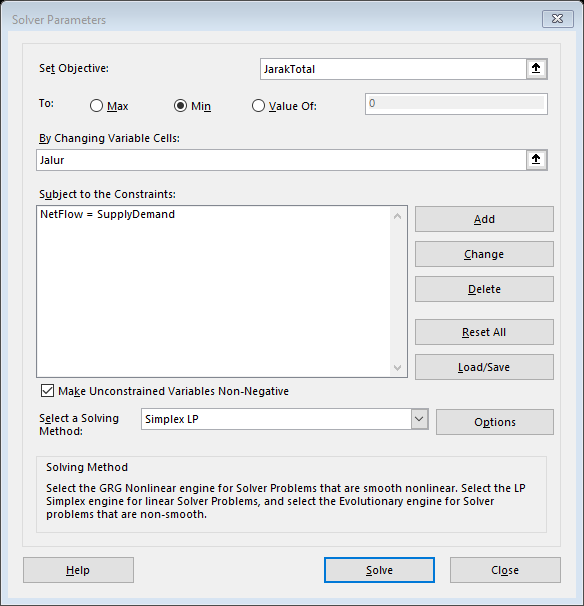
Masuk ke Data > Solver. Atur parameter sebagai berikut:
- Set Objective: Klik sel JarakTotal[cite: 152].
- To: Pilih Min (karena kita mencari rute paling dekat/singkat)[cite: 152].
- By Changing Variable Cells: Sorot sel kosong pada kolom Jalur (Keputusan)[cite: 152].
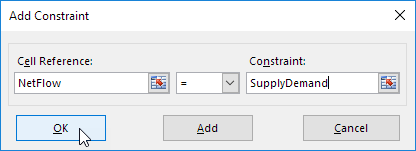
- Constraints: Tambahkan aturan mutlak bahwa nilai kolom Net Flow harus sama dengan (
=) nilai pada kolom Supply/Demand (yaitu aturan 1, -1, dan 0 yang kita buat di langkah sebelumnya)[cite: 153].
Langkah 4: Solve! Temukan Rute Tercepat Anda
Pastikan Anda mencentang ‘Make Unconstrained Variables Non-Negative’, pilih ‘Simplex LP’, dan klik Solve[cite: 154].
BAM! Navigasi Rute Ditemukan
Solver akan mengubah sel rute yang terpilih menjadi angka 1. Mengikuti jalur angka 1 tersebut, kita menemukan rute tercepat adalah:
Start ➡️ S ➡️ A ➡️ D ➡️ C ➡️ T
Jarak Tempuh Paling Minimum:
11 [cite: 156]
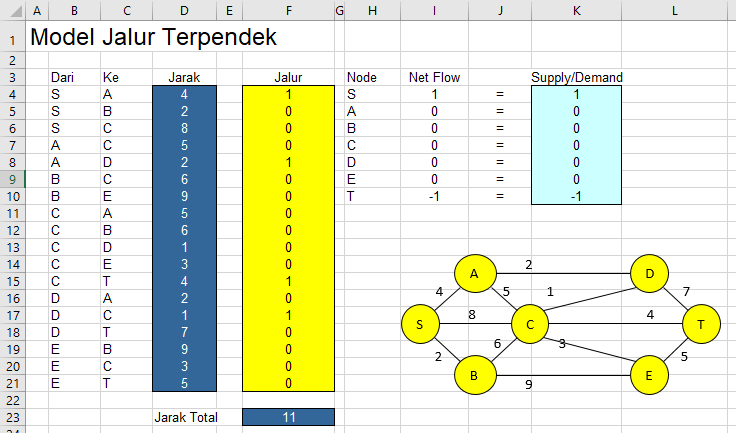
Hebat sekali! Anda tidak perlu repot-repot menghitung kombinasi jarak di peta secara manual. Solver langsung memberikan rute dengan pemotongan kompas (shortcut) paling optimal. Fitur ini sangat cocok diterapkan jika bisnis Anda menggunakan armada logistik, delivery order, maupun distribusi ke agen.
📚 Referensi Lengkap:
Untuk mendalami teori akademis dan melihat langkah teknis selengkapnya dari materi ini, Anda dapat mengunduh dokumen asli “Pemanfaatan Excel-Solver Untuk Pengambilan Keputusan” karya Bapak Aurino Djamaris melalui:
Repository Universitas Bakrie
Di artikel selanjutnya (Bagian 7), kita akan membahas topik yang berkebalikan namun sama menariknya, yaitu Model Aliran Maksimum (Maximum Flow). Pastikan Anda terus memantau *update* terbaru di blog AurinoWorks!