Seri Panduan Bisnis – Bagian 7

Memaksimalkan Kapasitas: Model Aliran Maksimum (Maximum Flow)

Diadaptasi dari Bab VI modul “Pemanfaatan Excel-Solver Untuk Pengambilan Keputusan” (Aurino Djamaris).

Dalam infrastruktur bisnis, setiap rute atau saluran pasti memiliki daya tampung maksimal (kapasitas). Mulai dari batasan berat muatan jalan raya, jadwal terbang maksimal di sebuah bandara, hingga kapasitas maksimal pipa saluran air minum.

Pertanyaannya: Berapa banyak jumlah maksimal (volume/arus) yang bisa kita kirimkan dari titik awal (Start) ke titik akhir (Target) melalui berbagai persimpangan, tanpa ada satupun jalur yang jebol melebihi kapasitasnya?

Formulasi Model Jaringan Terarah

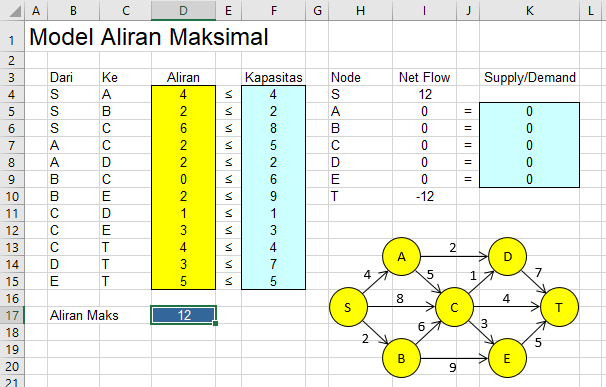
Dalam panduan Djamaris, kita membuat tabel yang berisi:

Jalur (Arc): Dari Node mana ke Node mana (misalnya dari Titik A ke Titik B).
Kapasitas: Batas maksimal yang bisa lewat di jalur tersebut.
Aliran (Flow): Sel kosong (Variabel Keputusan) yang nanti akan diisi oleh Solver untuk menentukan berapa banyak volume yang boleh lewat.

Tugas kita: Memaksimalkan nilai “Aliran”, namun dengan syarat tidak boleh melebihi “Kapasitas” masing-masing jalur.

Tabel Formulasi Model Aliran Maksimum yang berisi kolom Dari, Ke, Aliran, dan Kapasitas

Langkah Praktis: Rumus Keseimbangan Arus

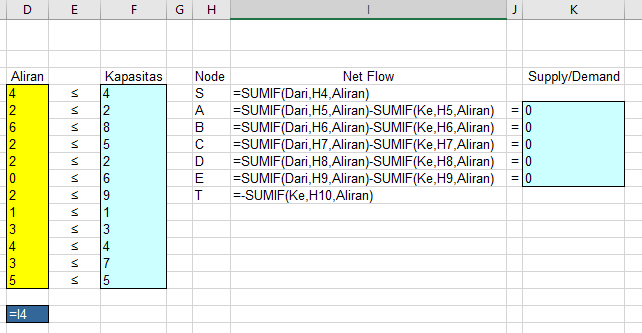
Agar barang/volume tidak “mengendap” atau hilang di persimpangan jalan, kita harus menggunakan rumus Net Flow (Arus Keluar – Arus Masuk) menggunakan fungsi SUMIF.

Aturannya sangat ketat: Untuk setiap titik persimpangan (Node A, B, C, D, dan E), jumlah barang yang masuk harus sama persis dengan jumlah barang yang keluar. Dengan kata lain, Net Flow harus sama dengan 0.

Sel target kita (Fungsi Tujuan) adalah Aliran Maksimum, yang nilainya diambil langsung dari total arus yang berhasil keluar dari titik Start (S).

penggunaan fungsi SUMIF untuk menghitung Net Flow setiap node

Mengatur Parameter Solver

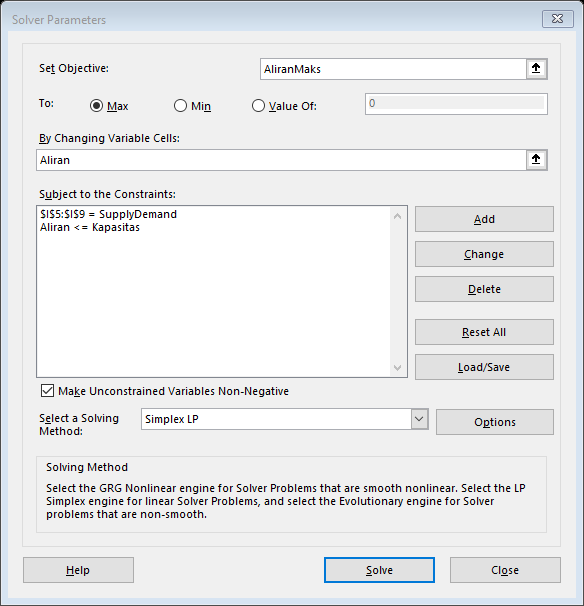
Buka Data > Solver. Kali ini kita kembali menggunakan target Maksimalisasi, dengan pengaturan pembatas (Constraint) sebagai berikut:

Set Objective: Klik sel AliranMaksimum.
To: Pilih Max.
By Changing Variable Cells: Sorot sel kosong pada kolom Aliran.
Constraint 1 (Keseimbangan): Net Flow persimpangan (A, B, C, D, E) harus sama dengan (=) 0.
Constraint 2 (Kapasitas): Nilai kolom Aliran harus kurang dari atau sama dengan (<=) nilai di kolom Kapasitas.

kotak dialog Solver Parameter yang menunjukkan kedua Constraint di atas ditambahkan

Solve! Temukan Kapasitas Puncak Anda

Pastikan Anda mencentang ‘Make Unconstrained Variables Non-Negative’, pilih ‘Simplex LP’, dan klik Solve.

BAM! Jaringan Bekerja Maksimal

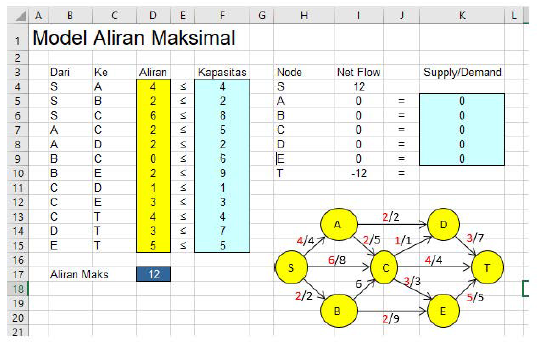
Berdasarkan kesimpulan Bapak Aurino, Solver membagi arus ke berbagai jalur agar tidak terjadi penumpukan:

Jalur SADT mengalirkan 2 unit
Jalur SCT mengalirkan 4 unit
Jalur SBET, SCET masing-masing 2 unit
Jalur SACET, SACDT masing-masing 1 unit

Total Aliran Paling Maksimum:
12 Unit

tabel solusi optimal Kapasitas Puncak di lembar Excel

Fantastis! Dengan memanfaatkan Excel Solver, Anda tidak perlu khawatir ada jalur distribusi yang kelebihan beban (overload) hingga membahayakan infrastruktur bisnis. Seluruh kapasitas berhasil digunakan hingga mencapai potensi tertingginya.

📚 Referensi Lengkap:
Untuk mendalami teori akademis dan melihat langkah teknis selengkapnya dari materi ini, Anda dapat mengunduh dokumen asli “Pemanfaatan Excel-Solver Untuk Pengambilan Keputusan” karya Bapak Aurino Djamaris melalui:
Repository Universitas Bakrie

Selamat! Kita telah menyelesaikan berbagai studi kasus operasional fisik. Di Bagian 8 selanjutnya, kita akan memasuki level finansial (keuangan): Model Keputusan Investasi Modal (Capital Investment). Bagaimana menentukan pilihan proyek agar Return on Investment (ROI) perusahaan maksimal? Tunggu artikelnya di AurinoWorks!